اشتباههای مصطلح و به ظاهر درست، اما نادرست!
گاهی به اصطلاحی برخورد میکنیم که به ظاهر اشکالی در کاربرد آن وجود ندارد، اما وقتی به معنای آن دقت میکنیم، به اشتباه خود پی میبریم.
برای روشن شدن مطلب، پرسشی را مطرح میکنم. آیا در بیان «نوسان دورهای» اشتباهی وجود دارد؟ ظاهراً پاسخ این پرسش، منفی است. اجازه دهید کمی به عقب برگردیم و به معنای دو مفهوم فیزیکی «حرکت دورهای و حرکت نوسانی» توجه کنیم.
حرکت دورهای
در بررسی ویژگی حرکتها، مشاهده میکنیم که حرکتی وجود دارد که مشخصههای آن بعد از گذشت زمانهای معین و ثابتی به نام دوره (یا دوره تناوب) از هر نظر تکرار میشوند. به این حرکتها، حرکت دورهای گفته میشود. در حرکت دورهای، وقتی جسم از یک نقطة مسیر میگذرد، نیروی وارد بر آن، شتاب و سرعت جسم، اندازة معین و مشخصی دارند و هر کدام در جهت معینی هستند. بعد از گذشت زمان ثابتی به نام دوره که متحرک دوباره از همان نقطه و در همان جهت میگذرد، این کمیتها، همان اندازه و در همان جهت قبلی هستند. گردش ماه به دور زمین، گردش الکترون به دور هستة اتم در الگوی اتمی بور، نمونههایی از حرکت دورهای هستند.
حرکت نوسانی
در بین حرکتهای دورهای، به حرکت بعضی جسمها برخورد میکنیم که روی مسیر واحدی به صورت رفت و برگشت حرکت کرده و آن را تکرار میکنند. به این حرکتها، «حرکت نوسانی» یا به طور ساده «نوسان» گفته میشود. مانند حرکت رفت و برگشتی آونگ و حرکت سامانة «وزنه ـ فنر» روی سطح افقی و بدون اصطکاک.
اکنون به پاسخ پرسش ابتدای بحث، توجه کنید.
بیان «نوسان دورهای» دارای دو اشکال است:
اول آنکه چون دورهای بودن، ذاتی نوسانی است، کاربرد واژة «دورهای» تأکیدی بیجا و اضافی است. همانگونه که همة انسانها، قلب دارند و انسان بدون قلب وجود ندارد، و ما نمیگوییم «انسانِ قلبدار».
دوم و مهمتر آن که بیان «نوسان دورهای» به ذهن شنونده این را متبادر میکند که حتماً «نوسانهایی نیز وجود دارند که غیردورهای« اند، در حالی که نوسان غیردورهای وجود ندارد. تصور کنید که دانشآموز هوشمند و کنجکاوی از معلم خود بخواهد که «یک نوسان غیردورهای» را معرفی کند! پاسخ معلم چه خواهد بود؟
بنابراین، کاربرد اصطلاح «نوسان دورهای» اشتباه است و باید از بیان آن، جداً اجتناب کرد.
به همین ترتیب، ممکن است به اشتباههای فیزیکی دیگری برخورد کنیم. یکی از این اشتباهها، آن است که گاهی بیان میشود «بنا به قانون اول نیوتون دربارة حرکت، اگر برآیند نیروهای وارد بر جسمی صفر باشد، حرکت آن جسم یکنواخت روی خط راست خواهد بود. این، نه یک اشتباه که یک غلط علمی است.
اول آن که بنا به قانون دوم نیوتون دربارة حرکت، اگر برآیند نیروهای وارد بر جسمی صفر شود، شتاب حرکت آن جسم صفر و حرکتش، یکنواخت روی خط راست میشود. یعنی، قانون اول نیوتون با بیان بالا، نتیجهای از قانون دوم او دربارة حرکت خواهد شد و میدانیم که یک قانون نمیتواند نتیجهای از قانون دیگر باشد که در این صورت، دیگر قانون نیست.
دوم آنکه بیان نیوتون دربارة قانون اول به صورت زیر است:
«اگر به جسمی نیرو وارد نشود، برای ادامة حرکت به نیرو نیاز ندارد».
توجه به این نکته، مهم و ضروری است که قانون اول نیوتون بیان میکند که به جسم اصلاً نیرو وارد نشود، نه این که برآیند نیروهای وارد بر آن صفر باشد. نیوتون در بیان قانون اول، بسیار هوشمندانه (شاید هم زیرکانه) عمل کرده است.
قانون اول نیوتون بیانگر آن است که اگر به جسم نیرو وارد نشود، حرکت آن با سرعت ثابت، یعنی حرکت یکنواخت روی خط راست میشود.
شاید نیوتون مجبور بود اعتقاد قدیمی که بیان ارسطو است را از ذهنها پاک کند. بیان ارسطو آن بود که اگر بخواهیم جسمی با سرعت ثابت حرکت کند، باید به آن نیروی ثابتی وارد شود.
قانون اول نیوتون به وضوح بیان میکند که جسم با هیچ جسم دیگری در کنش نباشد، یعنی به آن هیچ نیرویی وارد نشود.
قانون اول دربارة حرکت، آنگونه که نیوتون، خود توضیح میدهد، ویژگی دستگاه مختصاتی را مشخص میکند که به آن، «دستگاه مختصات لخت» میگوییم. از نیوتون پرسیده میشود که شتاب، کمیتی نسبی و مقایسهای است (اگر اشتباه نکنم، شخصی به نام ولینگتون)، شتابی که در قانون دوم از آن نام میبری، در چه دستگاه مختصاتی است؟ نیوتون در پاسخ میگوید، «دستگاه مختصات لخت که ویژگی آن را در قانون اول بیان کردهام!
اگر در یک دستگاه مختصات، به یک جسم هیچ نیرویی وارد نشود و حرکت جسم در آن دستگاه با سرعت ثابت باشد، چنین دستگاهی، دستگاه مختصات لَخت نامیده میشود.
قانون دوم نیوتون باید در دستگاه لَخت به کار برده شود.
نیوتون، هوشمندانه در کتاب اصول خود، واضع قانونهای حرکت و قانون گرانش است. به طوری که اینشتین میگوید «کتابی به عظمت کتاب اصول نیوتون نوشته نشده و نخواهد شد.»
از نیوتون پرسیده میشود که «چگونه تو این همه چیز را میدانی و توضیح میدهی؟ نیوتون در پاسخ میگوید «من روی دوش غولها ایستادهام».
به جرأت میتوان گفت که غولهای مورد اشارة نیوتون، کسانی چون ابنسینا، گالیله و … هستند. بد نیست این بیان ابنسینا را در اینجا بازگو کنم که میگوید «اگر جسمی را به بالا پرتاب کنیم و هیچ قوّهای (نیرویی) آن را به زیر نکشد، تا سقف فلک پیش خواهد رفت». آیا این بیان، همان قانون اول نیوتون دربارة حرکت، نیست؟
این گفتة متواضعانة نیوتون هم شنیدنی است که میگوید:
من بسان کودکی میمانم که در کنار ساحل با گوش ماهیها بازی میکند، غافل از غوغای اقیانوس.
دنبالة بحث:
توجه به این نکته ضروری است که در پاسخ به پرسشهای مکانیک و حل مسألههای آن، مجبور به استفاده از قانونهای نیوتون دربارة حرکت نیستیم و میتوان از قانونهایی که توسط دیگران بیان شدهاند، استفاده کرد. یکی از این قانونها، توسط دالامبر بیان شده و به نام خود او «اصل دالامبر» نام دارد. در اصل دالایر، با وارد کردن نیرویی مجازی به جسم، مسألة دینامیکی را به استاتیکی تبدیل کرده و به پرسشها و مسألهها پاسخ میدهیم.
در نظر بگیرید که قطاری با شتاب ثابت روی ریلهای افقی و مستقیم در حرکت است و آونگی ساده از سقف واگن آویزان شده و نوسان نمیکند. آونگ در خلاف جهت شتاب قطار با زاویة نسبت به وضع قائم میایستد. (شکل 1 را ببینید).
میخواهیم زاویة را به کمک اصل دالامبر، محاسبه کنیم.
فرض میکنیم میدانی درون واگن وجود دارد که به هر جسم به جرم نیرویی به بزرگی در خلاف جهت شتاب وارد میکند. این میدان را میدان لختی (میدان اینرسی) و به نیروی نیروی لختی میگوییم.
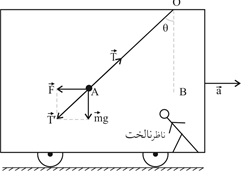
شکل (1)
نیروی واقعی وارد بر گلولة آونگ، یکی نیروی وزن است که از طرف میدان گرانش زمین به آن وارد میشود و دیگری نیروی کشش نخ است. چون آونگ آویزان و نسبت به واگن ساکن است، برآیند نیروهای وزن و نیروی لختی ، هماندازه و در خلاف جهت کشش نخ خواهد بود. درواقع ناظر درون واگن (که ناظر نالخت است)، برای توجیه سکون آونگ نسبت به خود، نیروی مجازی را به آونگ وارد میبیند تا برآیند نیروهای وارد بر آونگ صفر شود.
با توجه به شکل 1 میتوان نوشت:
همانگونه که گفته شد، نیروی لختی از دید ناظر ساکن در واگن وجود دارد، چنین ناظری، نیروی لختی را احساس میکند. او برای اثبات وجود نیروی لختی ، آونگ را به وضع قائم (نسبت به زمین، راستای ) میآورد و رها میکند، دیده میشود که آونگ به وضع آنچه که در شکل 1 نشان داده شده است، میرود.
از دید ناظر ساکن بر زمین در کنار ریل، چنین نیرویی (نیروی لختی ) وجود ندارد. به این ناظر، ناظر لخت میگوییم. ناظر لخت، نیروهای واقعی را میبینید و از قانونهای نیوتون دربارة حرکت استفاده کرده و مسأله را حل میکند.
ناظر لخت، نیروهای وزن آونگ و کشش نخ را میبیند (شکل 2) که برآیند آنها به آونگ شتاب (هم اندازه و در جهت شتاب واگن) میدهد، از دید این ناظر داریم:
به شکل 2 وضع ایستادن ناظر لخت و ناظر نالخت توجه کنید.
به این نکته نیز توجه کنید که ناظر نالخت (یعنی ناظری که برآیند نیروهای وارد بر او، صفر نیست)، حق استفاده از قانونهای نیوتون دربارة حرکت را ندارد. اگر چنین ناظری از قانونهای نیوتون استفاده کند و خود را ساکن پندارد، به جسم، نیروی مجازی (نیروی نالخت) وارد میبیند.
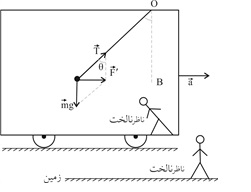
شکل (2)
غلامعلی محمودزاده
آذر ماه 1399